We are making available an algorithm for monotone fast iterative shrinkage-thresholding (MFISTA) with variable acceleration (VA) that reduces reconstruction time of compressed sensing MRI.
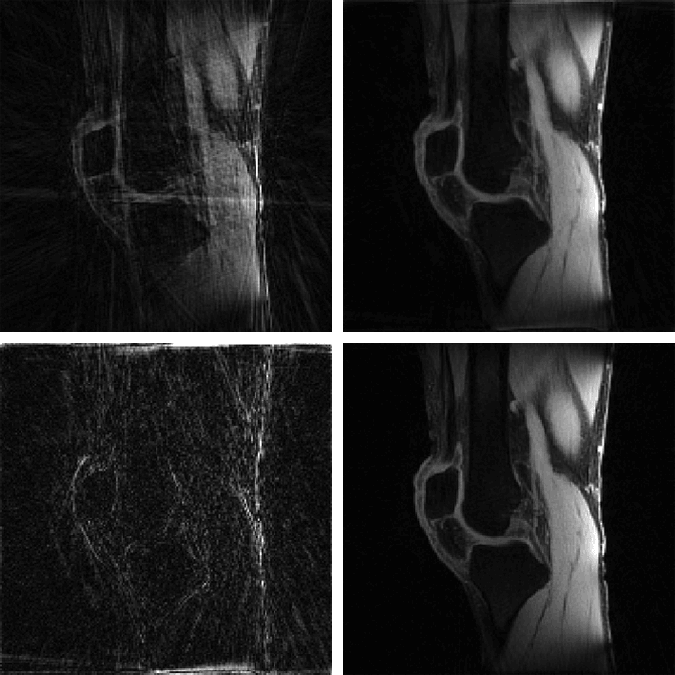
The MATLAB codes contain implementation of the proposed MFISTA-VA, as well as versions of FISTA, MFISTA, and OISTA, for compressed sensing in magnetic resonance imaging. The codes are comprehensive and ready to apply on low rank, sparse, and low rank plus sparse (L+S) problems. Examples are given with radial T1ρ knee and liver data from NYU Langone Health. Coil sensitivity maps were obtained with ESPIRiT.
For more information, see the related publication and references.
Related Publication
Monotone FISTA with Variable Acceleration for Compressed Sensing Magnetic Resonance Imaging.
IEEE Trans Comput Imaging. 2019 Mar;5(1):109-119. doi: 10.1109/TCI.2018.2882681
Please cite this work if you are using MFISTA-VA in your research.
References
A fast iterative shrinkage-thresholding algorithm for linear inverse problems.
SIAM J Imaging Sci. 2009;2(1):183-202. doi: 10.1137/080716542
Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems.
IEEE Trans Image Process. 2009 Jul 24;18(11):2419-34. doi: 10.1109/TIP.2009.2028250
An optimized first-order method for image restoration.
2015 IEEE International Conference on Image Processing (ICIP). 2015 Sep 27 (pp. 3675-3679). doi: 10.1109/ICIP.2015.7351490
Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components.
Magn Reson Med. 2015 Mar;73(3):1125-36. doi: 10.1002/mrm.25240
ESPIRiT–an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA.
Magn Reson Med. 2014 Mar;71(3):990-1001. doi: 10.1002/mrm.24751
On NUFFT-based gridding for non-Cartesian MRI.
J Magn Reson 2007 Oct;188(2):191-5. doi: 10.1016/j.jmr.2007.06.012
Get the Code
The software available on this page is provided free of charge and comes without any warranty. CAI²R and NYU Grossman School of Medicine do not take any liability for problems or damage of any kind resulting from the use of the files provided. Operation of the software is solely at the user’s own risk. The software developments provided are not medical products and must not be used for making diagnostic decisions.
The software is provided for non-commercial, academic use only. Usage or distribution of the software for commercial purpose is prohibited. All rights belong to the author (Marcelo Wust Zibetti) and NYU Grossman School of Medicine. If you use the software for academic work, please give credit to the author in publications and cite the related publications.
Contact
Questions about this resource may be directed to Marcelo Wust Zibetti, PhD.
